Examining “Ben Graham's Net Nets: Seventy-Five Years Old and Outperforming”
- Gaurang Merani

- Oct 25, 2020
- 14 min read
Updated: Nov 4, 2020
Introduction
The focus of this analysis is the research paper “Ben Graham's Net Nets: Seventy-Five Years Old and Outperforming” by Tobias Carlisle, Sunil Mohanty, and Jeffrey Oxman[i] published in 2010. The objective of the paper was to provide an update on the research conducted by Henry R. Oppenheimer in his 1986 study titled, “Ben Graham’s Net Current Asset Values: A Performance Update.” (We examined Oppenheimer’s research in our article, “An Analysis of Benjamin Graham’s Net Current Asset Values: A Performance Update”.) Following the methodology adopted in Oppenheimer’s study, the authors selected securities that were trading at no more than two-thirds of their Net Current Asset Value (NCAV). Their 25 year examination period ran from 31 December 1983 to 31 December 2008 and they focussed on US listed securities.
Our objective was to analyze the study itself; determine its reliability, draw our own conclusions and glean, if any, actionable advice for the practitioner of the NCAV method of investing.
We have previously published a number of posts with regard to securities trading at less than their Net Current Asset Value including:
Key Methodology
Valuation metric:
“…sum of all liabilities and preferred stock and subtracted it from current assets; this result was then divided by the number of common shares outstanding.”
i.e. Net Current Asset Value per share = (Current Assets – (Total Liabilities + Preferred Shares))/Common Shares Outstanding
“…bought a security if its November closing price was no more than two-thirds of its NCAV”
Weighting of holdings: “equal-weighted”
Purchase/rebalance date: “December 31st”
Holding period: “held for one year” and “held for 30 months”
Reliability
Studies can suffer from a number of issues which reduce their reliability. Below we address potential concerns around sample size, return calculation methodology, data sources and common biases that may afflict research:
1. Sample size, exchanges and firm characteristics
From 1984 to 2008 the number of firms meeting the necessary criteria ranges from 13 to 152 with an average of almost 55 firms. Relative to other studies, this study contains a far larger sample of firms.
Exhibit 1 is reproduced below:

No industries or sectors were excluded from the study. No minimum market capitalization was specified. Consequently, the inclusion of the smallest firms could have unduly influenced results as even when investing relatively modest sums the securities of the very smallest firms are virtually untradeable.
2. Return calculation methodology
The authors calculated and reported the “Mean Returns”. In academic research (such as this) returns are often measured by calculating the arithmetic mean return (as opposed to the geometric mean return) - this appears to be the case in this study. It should be noted that in a dependant return series that exhibits volatility (like stock returns) the arithmetic mean will, as a matter of mathematical law, overstate returns relative to the more practitioner oriented geometric mean. The magnitude of the potential divergence between the two measures is unknown given the data made available in the study.
We will examine this further in the next section.
3. Data source
Under the “Data and Methodology” section no mention of a data source was made. In the “Results” section the following was stated: “While Oppenheimer uses the Ibbotson Small-Firm Index, we use the smallest decile of stocks traded in the CRSP database.” This implies the study was conducted using Center for Research in Security Prices (CRSP) data. Presumably then, the fundamental data came from Compstat based on the “CRSP/Compustat Merged Database”, however, this is assumed and not stated in the study.
The Center for Research in Security Prices (CRSP) database is considered to be the gold standard for research.
4. Survivorship bias
The authors presumably used the CRSP database which includes data on delisted stocks. However, the delisted company data needs to be incorporated into the return data. An algorithm that mergers the CRSP delisting information into the returns is identified in the paper “Delisting Returns and Their Effect on Accounting-Based Market Anomalies,” by Richard Price, William Beaver and Maureen McNichols[ii]. However, it is not clear if the delisting data was merged into the return data used in this study.
Given that no specific mention was made with regard to controlling for survivorship bias it is possible, though not probable, that the study may have suffered from such a bias.
5. Look Ahead bias
They “bought a security if its November closing price was no more than two-thirds of its NCAV”. Presumably, the November NCAV was based on financial statement data related to the previous 30 September (or perhaps previous 30 June). “We assume all stocks are purchased on December 31st”.
For clarity, a firm needed to meet the 2/3 of NCAV criteria based on its price on 30 November, however, the returns thereto were measured using its market price at 31 December.
Based on the above the study does not appear to suffer from look-ahead bias.
6. Time period bias
The study spans 25 years and we classify this as a “more reliable” period.
For reference:
< 10 years; inadequate/unreliable
11 to 20 years; somewhat reliable
> 20 years; more reliable
> 40 years; most reliable
7. Human error
There is nothing specified in the research methodology that would make us believe this study is at greater risk of suffering from human error.
8. Journal rating/credibility[iii]
This study was not, to our knowledge, published in a top tier academic journal and therefore cannot be granted the “additional credibility” that may come with such publication.
Reliability Assessment: Despite the relatively long time period (25 years) and relatively large sample size, due to the presentation of the arithmetic mean return (i.e. “Mean Return”) we would not place reliance on the results of the study from a practitioner’s standpoint. Also of concern is that no minimum market capitalization was specified for the securities examined. Consequently, the inclusion of the smallest firms may have unduly influenced results as even when investing relatively modest sums the securities of the very smallest firms are virtually untradeable.
Results and Analysis
While this study purported to be an update of Oppenheimer’s 1986 study unfortunately it did not contain the corresponding tables. Specifically, the most useful table from Oppenheimer’s study was Table IV which displayed the return in each year of the study and presented the “Annual Geometric Mean Return”. The “Annual Geometric Mean Return” represented the actual return potentially achievable in practice (gross of commissions and taxes).
12 Month Holding Period
“Exhibit 2 summarizes the results for the 25-year period of the study”, which deals with the 12 month holding period:


We note that the table heading states it is a “26” year period, however the study covered 25 years.
They present “monthly” “Mean Returns” (i.e. arithmetic mean). Exhibit II does indeed replicate the data presented in Table II of Oppenheimer’s study. Furthermore, based on reconciliation work carried out in “An Analysis of “Benjamin Graham’s Net Current Asset Values: A Performance Update”, it reinforces our view that the arithmetic mean returns have also been presented in this case.
“The mean monthly return on stocks meeting the NCAV rule in the period we examined, December 31, 1983 to December 31, 2008, was 2.55%. The mean monthly returns for the NYSE-AMEX and Small-Firm indices were 0.85% and 1.24% respectively. This indicates an outperformance by the NCAV portfolio over the NYSE-AMEX Index of 1.70% per month, or 22.42% per annum and an outperformance over the Small-Firm Index of 1.31% per month, or 16.90% per annum.”
“Panel C presents results for nine consecutive sub-periods, eight of which are of approximately equal length, and the final of which is incomplete.” It is unclear how the aforementioned reconciles to the data in Panel C which appears to commence and end with a 2 year period.
30 Month Holding Period
30 month holding periods are examined and presented in Exhibit III (reproduced below). The authors state “Graham suggested that a 30-month holding period was appropriate for the NCAV investment practice, rather than the twelve month period we have assumed thus far. Since the 30-month portfolios overlap each other, we create each using unique stocks. Thus, no two portfolios contain the same company’s shares. We assume, as above, that the portfolios are created on December 31st of each year, and then held for 30 months. However, portfolios created in 2006 have only 24 months of observations, and portfolios created in 2007 have only 12 months of observations. Rather than eliminate these years from the study, we report results with the above caveat in mind.”



At first glance Exhibit III, through its measurement of the “Terminal Wealth of $10,000” appears to be the representation of the actual dollar return achievable by an investor in practice (i.e. geometric mean/compounded return). However, like we discovered in An Analysis of “Testing Benjamin Graham’s Net Current Asset Value Strategy in London” and What Has Worked in Investing (Tweedy, Browne) – Examining Net Nets researchers “compounded” the arithmetic mean in attempt to put the returns in more “meaningful terms”. Indeed, we believe this to be the case in this study also. For instance, the 1983 monthly mean return of 3.59% when compounded for the stipulated 30 months with a starting value of $10,000 yields (rounding aside) the reported ~$28,846.24 (10,000*(1.0359)^30). When 3.59% is compounded monthly it results in an annualized (i.e. compounded) return of 55.7% ((28,846.24/10,000)^(12/30)-1). Similarly, in 1993 the reported monthly mean return was “7.97%”. When $10,000 is compounded for 30 months at 7.97% it yields (rounding aside) the reported ~$99,867.78 (10,000*(1.0797)^30). When 7.97% is compounded monthly it results in an annualized (i.e. compounded) return of 151.1% ((99,867.78/10,000)^(12/30)-1).
The implied returns are as extraordinary as they are illusionary!
Earnings and Dividends
“According to Oppenheimer, Graham frequently recommended that it was best to select NCAV securities that had positive earnings and paid a dividend. Oppenheimer’s findings seem to contradict this advice. He found that firms operating at a loss seemed to have slightly higher returns and risk than firms with positive earnings. Firms with positive earnings paying dividends provided a lower mean return than portfolios of firms with positive earnings not paying a dividend, but had a lower systematic risk. These findings led Oppenheimer to conclude that choosing only firms that have earnings and pay a dividend will not help the investor.
Our results, presented in Exhibit 4, support Oppenheimer’s conclusion. Firms with positive earnings generated monthly returns of 1.96%. By contrast, firms with negative earnings generated monthly returns of 3.38%. Firms with positive earnings paying dividends in the preceding year provided monthly returns of 1.48%, a lower mean return than portfolios of firms with positive earnings with no dividend paid in the preceding year (2.42%), but did have a lower systematic risk.”
In our analysis of Oppenheimer’s paper, (“An Analysis of “Benjamin Graham’s Net Current Asset Values: A Performance Update”) we identified that the research had been conducted with data that excluded dividends. Therefore, the conclusion reached in that study, “Choosing only firms that have…. a dividend does not help the investor” was not considered reliable. Furthermore, as data excluding dividends was also used to measure the returns of “positive” and “negative” earning firms, no reliable conclusion in relation to the impact of earnings on the return of the securities examined could be ascertained from the results of Oppenheimer’s study either. Given the flaws in Oppenheimer’s study we do not consider the results reported in this study as reinforcing his conclusions. Rather, the results in this study need to be viewed in isolation of Oppenheimer’s findings.
Exhibit 4 is reproduced below:

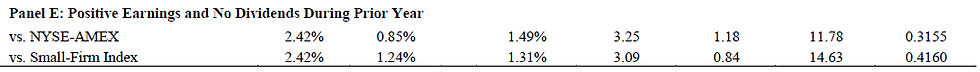
Having established that Oppenheimer’s results were compromised due to the exclusion of dividends we proceed by examining the same issue in this study.
The authors state, “Monthly returns are presented for the NCAV portfolios against various benchmarks, and sorted by earnings record and dividend payments. Rpt and Rmt are the NCAV portfolio and benchmark returns respectively….For all benchmarks, we use returns including dividends, except for the following: S&P 500, AMEX, and Nasdaq. These items are returns without dividends.” Why total returns (i.e. including dividends) weren’t used with regard to the S&P 500, AMEX, and Nasdaq is unknown. While portfolios may have been sorted by earnings and dividend payments it remains unclear whether the data used to measure the returns incorporated the dividend payments themselves.
“The results in this section indicate a rational connection between risk and return. Dividend-paying firms are viewed as less risky because the dividend signals to shareholders that managers believe the future cash flows of the firm are stable enough to accommodate an ongoing dividend.”
To accept the above conclusion an investor must also accept that “risk” is represented by the various “Risk Adjusted” measures presented, along with their implicit association with price volatility. Indeed, the acceptance of “beta” as an appropriate measure of risk adjusted returns runs contrary to the “low-beta anomaly”[iv].
Also, of concern is that no hypothesis (i.e. preceding the testing) was provided (in either study) for such results. Absent a more sound economic rationale for why positive earning non-dividend paying firms, 2.42% (and negative earning firms, 3.38%) would generate higher returns than positive earning dividend paying firms, 1.48% (and positive earning firms, 1.96%), data mining or the exclusion of dividends from the return data may provide greater explanatory power for the reported results compared to that provided within the study.
Valuation and Returns
Exhibit 5 and the corresponding narrative is reproduced below:

“Another question an investor may have is: does the depth of discount affect future returns? We have shown so far that the NCAV rule is an extreme form of value investing. A logical question comes up: do the deepest discounted NCAV stocks provide the highest returns in the future? To examine this, Oppenheimer calculated for each security its purchase price as a percentage of NCAV, and divided the population into quintiles according to this variable.”
“Adopting the same method, we analysed mean returns and risk-adjusted performance. The results are presented in Exhibit 5. Quintile 1 contains the fifth of the firms that have the highest discount, and Quintile 5 contains the firms trading closest to two-thirds of NCAV. With one caveat, our findings generally support Oppenheimer’s conclusion: the returns are higher for firms with higher discounts to NCAV. The caveat is as significant as it is perplexing: securities in Quintile 1– those with the lowest purchase price to NCAV – have the lowest returns. As noted earlier, we have eliminated as outliers firms with stock prices less than one percent of the NCAV per share, so we do not believe outliers are driving this result.”
“In results not reported here, we plot returns for each rank by year. No pattern exists in the ranked returns. Although the returns in rank 2 and rank 3 tend to be the highest, this is not always the case. So, we can say that on average there is a mild positive relationship between the depth of discount and future returns, there is such variability year-over-year that we cannot suggest this is a reliable rule.”
Some food for thought pertaining to the reported results: in general, value investing research[v] shows returns that are consistent with the relative “cheapness” of the underlying portfolios examined. Firms trading at less than 2/3 of NCAV would, almost certainly, consist of firms that in aggregate sit in the bottom decile of price to book (or by academic convention, top decile of book to market). Perhaps then, sorting these firms again based on discount to NCAV possesses limited utility; rather, other metrics (e.g. “quality measures”) may be required to eliminate the relatively poor performers. Indeed, in “Analyzing Deep Value in the Eurozone” we also observed that the firms that traded in the cheapest decile sorted by relative price to NCAV produced lower returns that those in the second cheapest decile.
As such then, we have no definitive explanation regarding the above results and only proffer thoughts for further contemplation.
Explanations for Excess Returns
The authors attempt to explain the “excess returns” by regressing a number of factors against the NCAV returns. For interested readers we recommend referring to the underlying paper, nonetheless, we cover the key statements below:
Market Risk
Unsurprisingly, they find “more than mere market risk explains the returns on the NCAV portfolios”.
Fama-French three factor model (Market/Size/Value)
“Applying the Fama-French three factor model to our data confirms the importance of the small-firm effect. All three factors are statistically relevant as explanatory variables, but the small firm effect is the largest factor.
They proceed and subsequently state: “However, there is still an economically significant excess return (alpha) of 1.67% per month. Assuming monthly compounding, this yields an excess return of 21.99% per year after controlling for market risk, the small-firm effect, and the book-to-market effect.” Why they “assume” compounding, when the returns calculated are actually “average” (i.e. arithmetic mean) returns remains unknown. However, the statement implies that the returns presented are “compounded returns” (i.e. geometric mean returns) which is misleading.
“[T]he value premium adds a minor [our emphasis] amount to the explanation of the results. The excess returns unexplained by market risk, the small firm effect, and the value premium remain positive and economically significant. Thus it appears that some other factor is at play in the generation of the outsized returns generated by the NCAV investing technique.”
It is interesting to note that purchasing firms trading below a NCAV (essentially an extreme form of price to book value) does not provide significant explanatory power, at least according to the regression analysis conducted.
Long Term Price Mean Reversion
“We apply the long-term reversal factor to our data …. While positive, the factor is not economically or statistically significant. Therefore, long-term reversal does not appear to explain the excess returns on NCAV portfolios.”
Momentum
“Since NCAV stocks are recent losers, we should expect the momentum factor to be negatively related to the returns on NCAV portfolios, and it is. It is also statistically significant – see Exhibit 7, Model 1 in Panel A [not reproduced here].” “What is especially interesting is that inclusion of the momentum factor washes out the significance of the value factor (HML), and causes it to change sign. This indicates that the momentum factor is an important variable in explaining returns on NCAV portfolios.”
Liquidity
“We add the liquidity measure in with the Fama-French 3 factors and the momentum factor, which was previously found to be significant, and estimate Model 5. Now we find HML and MOM are insignificant, and so discard these factors and estimate Model 6. The fit of this model is the highest of all those estimated, and so we are confident that the market risk, small-firm effect (SMB) and liquidity factors (ILLIQ) are the only [our emphasis] factors that explain the returns on the NCAV portfolios of the ones we have applied.”
The January Effect
“The January effect in our portfolios accounts for 10% of returns in the year, while the other eleven months account for about 2% each. Thus, the January effect is nearly half of the whole year’s return. This does not mean, however, that the January effect drives returns on the NCAV portfolios.”
Indeed, the results of the regression analysis may elicit a range of reactions from readers. Some readers may consider the results to be “objective and instructive” while a review of the results by other readers may evoke the quote “Lies, damned lies, and statistics”!
We leave it to readers to ascertain the utility, or otherwise, of that presented by the authors in this section.[vi]
Conclusion
“Ben Graham's Net Nets: Seventy-Five Years Old and Outperforming” was a study that covered the 25 year period from 31 December 1983 to 31 December 2008 and it focussed on US listed securities trading below two-thirds of their NCAV. In addition to examining the returns over a 12 and 30 month holding period respectively, the authors also attempted to explain the drivers of the observed excess returns by regressing various factors against the returns generated by the NCAV portfolios.
Their conclusion states “The results are as clear as they are compelling: Seventy five years on, Graham’s NCAV rule continues to identify securities that generate above-market returns.”
When looking at the findings reported in the paper from a practitioner’s point of view, our conclusion is different. The “mean returns” reported in the study were calculated as the arithmetic mean of returns which would have overstated the actual returns potentially achievable by an investor in practice. Without specification of the geometric mean return, which reflects practitioner reality, we cannot be certain of the actual return achieved. In addition, no minimum market capitalization was specified for the securities examined and consequently their inclusion may have unduly influenced the results as even when investing relatively modest sums the securities of the very smallest firms are virtually untradeable.
For the practitioner not afraid to be confronted with a conclusion that may be inconsistent with their prior beliefs, we offer our version of the authors conclusion based on our extensive analysis of the study:
“The results are as [unclear] as they are [overstated]: Seventy five years on, Graham’s NCAV rule continues to identify securities that [may] generate above-market returns, [we simply do not know based on the methodology adopted in this study].”
Notes:
[i] We contacted the corresponding author on a number of occasions to seek clarity on aspects of the study and never received a response, nor did we receive a response from the second listed author and the first listed author did not have in his possession the underlying data which we wished to review. [ii] Quantitative Value - Carlisle, Tobias, Gray, Wesley Ph.D., Chapter 10.
[iv] For research on Low-Volatility/Low-Beta see here: https://alphaarchitect.com/category/architect-academic-insights/factor-investing/low-volatility-investing/ [v] For further value investing research see here: https://alphaarchitect.com/category/architect-academic-insights/factor-investing/value-investing/
[vi] The same research team (Tobias Carlisle, Sunil Mohanty, and Jeffrey Oxman) authored the paper “Dissecting the Returns on Deep Value Investing” (2012) (https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1928694 ) in which they examined numerous factors in an attempt to “explain the returns” to firms trading below NCAV (albeit with a variation of the valuation methodology applied in this study).






Comments